Ballmer’s Guessing Game
John Graham-Cumming did some interesting analysis recently on a problem that Steve Ballmer had used for candidates interviewing at Microsoft. The gist of the problem is as follows:
Suppose a game host comes to you with the following challenge: They will choose a number between 1 and 100. During each turn of the game, you (the guesser) gets to guess a number. The host will then answer that their number is equal to, less than, or greater than the number you guessed. During the game, you will guess numbers until you get to the host’s number – if your first guess is right, you get \$5, then \$4, and so on until \$0, then -\$1, and so on.
Should you accept this challenge?
Ballmer’s initial claim is that the player should not – that if the player were to play a predictable strategy such as binary search, then the host can predict this and choose a number that intentionally takes long for binary search, then the host wins \$1.
Ballmer then incorrectly asserts that the expected value for the game is also negative, and the host wins, under the assumption that the host chooses a random number between 1 and 100 with uniform probability for any number. Graham-Cumming demonstrates with some proper math about expectations that this is incorrect, and the guesser should expect to win about \$0.2 on average.
However, if we want to be totally technically correct, neither of these answers are completely true. In a game where both the host and the guesser are trying to maximize their own payoff, computing the optimal strategy is actually quite difficult.
Optimal strategies#
Generally when we’re looking at “optimal strategies” for games like this, what we’d like is to find a unique Nash equilibrium. This is a strategy profile such that:
- If the host knew what strategy the guesser was using, the host would not change their strategy;
- If the guesser knew what strategy the host was using, they would not change their strategy either.
In adversarial zero-sum games like this, we know that we can apply the Minimax theorem. In layman’s terms, the “minimax outcome” is one that minimizes the most damage that your opponent can do to you. What this means is, if you’re playing a minimax strategy, your opponent has no strategy possible to make you lose worse in expectation than the expected payoff from the game.
It also provides two other nice assurances: First of all, we know this optimal strategy exists and the estimated payoff of that strategy is called the value of the game. Secondly, there are better computational method for solving minimax equilibria, which means for us we’re not running into any intractable computations.
The strategy profiles we’ll be looking at are mixed strategies – in other words, we’re going to end up with a strategy like “the host chooses 1 with 2% probability, 2 with 4%, …, 100 with 3%”. This is in contrast to pure strategies, which can be eliminated trivially since if we only chose one number and our opponent knew that number, they would always be able to choose their own preferred outcome.
A lower bound estimate#
First of all, let us make a small addendum to the game: We will allow the host to “pick” a new number every turn if the guesser is wrong, but it must be subject to the constraints previously stated. For example, in this variant the following could happen:
- The host picks 52.
- The guesser picks 50, and the host says the number is greater.
- The host picks a new number between 51 - 100: 63.
- The guesser picks 75, and the host answers it is less.
- The host picks a new number between 51 - 74: 61.
- The guesser picks 61 and wins – the guesser wins \$3.
I am making this modification as, since this game involves a sequential set of decisions, it helps our analysis to look at each turn of the game as a subgame so that we can benefit from some of the relevant theory.
This does mean that the host has slight leverage in this variant of the game. However, because the host has more decision power, the expected payoff for the guesser in this variant is a lower bound of the expected payoff in the general game. In other words – since the host is given more power in this game, any optimal strategy we derive will also work against the limited host, who is now forced to play a less-than-optimal strategy.
Minimax#
Since this game is now sequential and zero-sum (the sum of the payoffs of both players is always \$0), we can fortunately use the minimax theorem:
In any finite, two-player, zero-sum game, in any Nash equilibrium each player recieves a payoff that is equal to both his maxmin value and his minmax value.
See this paper by Mira Scarvalone for a proof of the minimax theorem as it relates to games.
The important part of our mimimax theory is that we can compute a unique and optimal estimated payoff for both players (called the “value” of the game).
Backwards induction#
In order to actually determine a winning strategy, we need to break it down into a tractible process. While it is possible to turn a sequential game into an equivalent simultaneous form game, in this case the action space is far too large to feasibly represent on a computer.
Fortunately, backwards induction can help us reduce the complexity. By working backwards from terminal subgames (i.e., when there are no subsequent turns) we can compute optimal strategies and use the estimated payoffs to generate simpler subgames recursively.
We can also reduce a significant amount of redundant computation by recognizing that most of the subgames in our lottery problem are repeated. For example, choosing from the ranges $[3,49]$ or $[51,97]$ are functionally identical; it is only the size of the range (in this case, 48) that affects the game itself.
From that principle, we can apply a dynamic programming-esque approach to our problem to solve the lottery challenge – by solving the game for $[1,1]$, then $[1,2]$, $[1,3]$ and so on until we reach $[1,100]$.
I will notate the estimated payoff for the host of each of these games as $P^h_n$, which would be equivalent to the host’s ($h$) expected payoff for the game $[1,n]$. The chooser’s payoff is $P^c_n$.
To illustrate this example, let’s solve the first three subgames. $[1,1]$ is trivial; since the only choice is $1$, the host and chooser must choose the same number. To ensure the final payoff for our host is the amount we need to deduct from the initial wallet size, we’ll say that guessing correctly means that both the host and the guesser have a payoff of $0$; i.e. $P^h_1=P^c_1=0$.
The subgame $[1,2]$ is simple. We structure the payoff matrix as follows (let’s assume the host’s actions are the rows and the chooser’s are the columns):
| 1 | 2 | ||
|---|---|---|---|
| 1 | $(0,0)$ | $(1,-1)$ | |
| 2 | $(1,-1)$ | $(0,0)$ |
In other words, whenever the guesser is wrong, they get \$1 deducted from their final reward, and the host gets \$1 back.
This is a combined version of the coordination/anti-coordination game where the host (row player) wants to avoid guessing the same and the chooser (column player) wants to coordinate.
The Nash equilibrium of this game is trivial; $p(1)=p(2)=0.5$ for both players. To verify this, we can simply observe that the expected payoff for both players is equal to $P^h_2=0.5$ and $P^c_2=-0.5$ respectively. For more information on verifying Nash equilibria, see this lecture.
Now let’s look at a more complex example: The 3x3 game.
| 1 | 2 | 3 | ||
|---|---|---|---|---|
| 1 | $(0,0)$ | $(P^h_1+1,P^c_1-1)$ | $(P^h_2+1,P^c_2-1)$ | |
| 2 | $(P^h_2+1,P^c_2-1)$ | $(0,0)$ | $(P^h_2+1,P^c_2-1)$ | |
| 3 | $(P^h_2+1,P^c_2-1)$ | $(P^h_1+1,P^c_1-1)$ | $(0,0)$ |
To explain the numbers: Suppose the host chooses $2$ and the chooser chooses $1$. This means that the new options are now $[2,3]$, which is identical to the $[1,2]$ game. Therefore, the expected payoff for the chooser is $P^c_2-1$; the chooser loses \$1 for making an incorrect guess and then receives the expected payoff for the result of the 2x2 game, i.e. $P^c_2$.
Since we already know these expected numbers, we can substitute them:
| 1 | 2 | 3 | ||
|---|---|---|---|---|
| 1 | $(0,0)$ | $(+1,-1)$ | $(+1.5,-1.5)$ | |
| 2 | $(+1.5,-1.5)$ | $(0,0)$ | $(+1.5,-1.5)$ | |
| 3 | $(+1.5,-1.5)$ | $(+1,-1)$ | $(0,0)$ |
Usually these types of systems are solved by framing it as a system of equations, or using a solver to generate an approximate solution. Most of this is a lot of annoying work and fairly complicated; fortunately, nashpy exists and provides a really nice set of tools for analyzing simultaneous games:
>> import numpy as np
>> import nashpy as nash
>> # write the payoffs for the host
>> A = np.matrix([[0,1,1.5],[1.5,0,1.5],[1.5,1,0]])
>> g = nash.Game(A)
>> print(g)
Zero sum game with payoff matrices:
Row player:
[[0. 1. 1.5]
[1.5 0. 1.5]
[1.5 1. 0. ]]
Column player:
[[-0. -1. -1.5]
[-1.5 -0. -1.5]
[-1.5 -1. -0. ]]
>> nash_eq = next(g.support_enumeration())
>> # this is the mixed strategy for the host and the guest
>> print(nash_eq)
(array([0.42857143, 0.14285714, 0.42857143]), array([0.28571429, 0.42857143, 0.28571429]))
>> # the host's mixed strategy as a fraction is [3/7, 1/7, 3/7]
>> # this is the expected reward for the host for each action
>> np.matmul(nash_eq[0][np.newaxis], A)
matrix([[0.85714286],
[0.85714286],
[0.85714286]])
>> # so the value of this game is 0.85714286, or about 6/7 for the host
>> # since this is zero sum, the value for the guesser is -0.85714286
Using this, I’ve written a small piece of logic that would in theory calculate the expected payoff for a generic game guessing for the range $[1,n]$:
from dataclasses import dataclass
import numpy as np
import nashpy as nash
import itertools
@dataclass(frozen=True)
class Payoff:
host: float
# the game is zero-sum, so it'll always be negative of the host
@property
def guest(self) -> float:
return -self.host
nash_eqs: list[tuple[(np.ndarray, np.ndarray)]]
# We'll populate our payoffs with the values for 0, 1, and 2.
_payoffs: dict[int, Payoff] = {
0: Payoff(host=0, nash_eqs=[]),
1: Payoff(host=0, nash_eqs=[]),
2: Payoff(host=0.5, nash_eqs=[(np.array([0.5, 0.5]), np.array([0.5, 0.5]))]),
}
def _calculate_host_payoff_matrix(n: int) -> np.ndarray:
"""
Calculate the n x n payoff matrix for the host, when guessing in the range
[1, n].
"""
A = np.zeros((n, n))
for i, j in itertools.product(range(n), range(n)):
# the host's/guest's choice is i+1, j+1
if i == j:
A[i, j] = 0
elif j < i:
# the guest's choice was j+1
# our new range is [j+2, n], with a length of n - j - 1
A[i, j] = get_payoff(n - j - 1).host + 1
else:
# the guest's choice
# our new range is [1, j], with a length of j
A[i, j] = get_payoff(j).host + 1
return A
def _calculate_payoff(n: int) -> Payoff:
"""
Calculate the value of the game for the host in the [1, n] game.
"""
# since the game is zero-sum, the guesser's payoff matrix is inferred
# from the host
A = _calculate_host_payoff_matrix(n)
g = nash.Game(A)
nash_eqs = []
# because our game is zero-sum, we can use something called the minimax
# theorem to find our equilibria. In practical terms this just means that
# they can be discovered using a linear program, which is much faster
# than most exponential-time methods for finding Nash equilibria
for nash_eq in g.linear_program():
nash_eqs.append(nash_eq)
# for now... just use the first one
break
# calculate the estimated payoff per host choice
host_payoffs_vec = np.matmul(nash_eqs[-1][np.newaxis], A.T)
# these are all the same... so just choose the first one
host_payoff = host_payoffs_vec[0][0]
# assert all payoffs are equal, just as some validation
assert np.all(np.isclose(host_payoffs_vec, host_payoff))
# technically we should also assert the same for guests... but I'm lazy
# so I'll assume nashpy is good
return Payoff(host=host_payoff, nash_eqs=nash_eqs)
def get_payoff(n: int) -> Payoff:
"""
This is the memoization function to reduce the number of needed computations
https://en.wikipedia.org/wiki/Memoization
"""
if n not in _payoffs:
_payoffs[n] = _calculate_payoff(n)
return _payoffs[n]
# Finally, compute the estimated payoff for the 100x100 game
final_payoff = get_payoff(100)
# The final payoff
print(final_payoff.host)
What’s the result?#
Ultimately, what I found was that the value of the final game was around $5.21$ – in other words, if the guest starts out with \$5, they will end up losing overall, by about -\$0.19 or so. Therefore, under the assumption that the host plays optimally per turn, we wouldn’t want to play this game.
Unfortunately since our estimate is a lower bound, we can’t really generalize it to the original game. Nonetheless, I’ve done some empirical evaluation to determine how our strategies perform in the original game and the evidence suggests that the distribution for the host’s choices on the initial guess are very hard to beat, and our “optimal” guesser strategy still performs best.
To keep this relevant (and to protect myself from the fact that I’ve spent several hours on this now) let’s just push that starting money up to \$6… then this all magically works again and we’ve got a guaranteed reward of around \$0.80!
What’s the strategy, though? Well, as one might expect, it’s very similar to binary search, but the distribution is much like a Beta distribution. In fact, it’s actually close enough that I probably will write something up to see if I can find the exact parameters to the beta distribution.
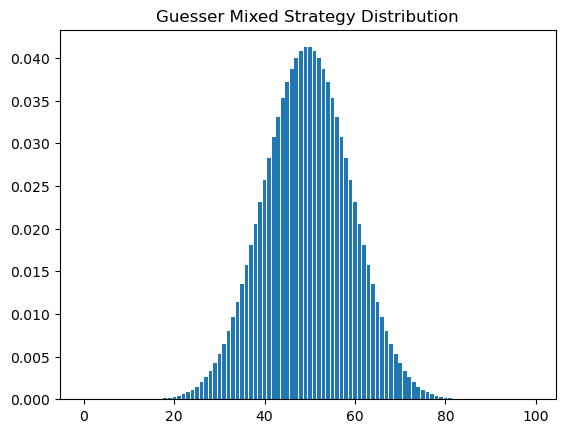
The host’s strategy distribution is a similar Beta distribution that favors the extrema:
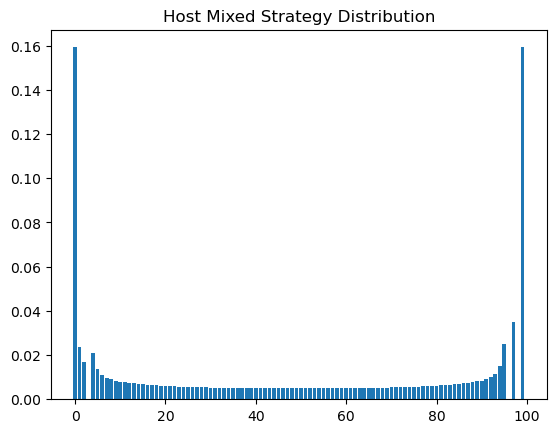
This is also a very interesting observation in regards to Bayesian reasoning; for those who are unaware, the Beta distribution is a conjugate prior to the Bernoulli distribution. I wouldn’t be surprised if this could instead be modeled as a probabilistic modeling and optimization problem from an entirely different set of priors and arrive at the same conclusion.
For another perspective, this is arguably also an example of an exploration vs. exploitation type of problem. In other words, the guesser needs to balance both maximally reducing the search space while also ensuring they have a good chance of getting the right number, because binary search alone isn’t good enough to save them.
Validations#
Fortunately, validation of Nash equilibria strategies is pretty simple. All we need to do is fix one of our players to the optimal strategy, and if the other player cannot change their payoff no matter what they do (and this is demonstrated in both directions) then it’s probably a Nash equilibrium.
Here is my own validation simulation below:
from typing import Literal
import numpy.random as npr
def simulate_game(host_strategy: Literal["optimal", "uniform", "midpoint", "once"]) -> int:
lbnd = 1
ubnd = 100
# this is the chooser's reward
reward = 6
host_choice = None
for _ in range(100):
reward -= 1
if host_strategy == "optimal":
# the host chooses a random valid number according to their strategy
ph = get_payoff(ubnd-lbnd+1).nash_eqs[0]
host_choice = np.random.choice(range(lbnd, ubnd+1), p=ph)
elif host_strategy == "uniform":
# the host chooses randomly with no preference
host_choice = np.random.choice(range(lbnd, ubnd+1))
elif host_strategy == "once" and host_choice is None:
# we'll pick one number and stick with it for the entire simulation,
# identical to the original game
host_choice = np.random.choice(range(lbnd, ubnd+1))
else: # if host_strategy == "midpoint":
# the host chooses the number directly in-between the current range
host_choice = int((lbnd+ubnd)/2)+1
# ensuring that we're always predicting a number between those bounds
assert host_choice >= lbnd and host_choice <= ubnd
# the chooser is going to select from the optimal probability distribution
pg = get_payoff(ubnd-lbnd+1).nash_eqs[1]
guest_choice = np.random.choice(range(lbnd, ubnd+1), p=pg)
if host_choice < guest_choice:
ubnd = guest_choice - 1
elif host_choice > guest_choice:
lbnd = guest_choice + 1
else:
return reward
if lbnd >= ubnd:
return reward - 1
# this should never happen
return None
# What we expect: All of these number should be approximately the same
print("Optimal:")
print(np.mean([simulate_game("optimal") for _ in range(50000)]))
print("Uniform:")
print(np.mean([simulate_game("uniform") for _ in range(50000)]))
print("Midpoint:")
print(np.mean([simulate_game("midpoint") for _ in range(50000)]))
print("Once:")
print(np.mean([simulate_game("once") for _ in range(50000)]))
This generated the following:
Optimal:
-0.2074
Uniform:
-0.20546
Midpoint:
-0.2134
Once:
-0.20188
(note: to be proper usually we wouldn’t just compare means… we would do statistical testing to measure our confidence that the results did not come from different distributions. but I’m just doing some quick validation here)
What we find is that under our strategy, the host’s choice makes no difference to our ultimate payoff, which empirically is what we’d expect with the minimax strategy or a Nash equilibrium.
Another validation worth trying is: Suppose the host makes a single choice at the start using the distribution we derived, and we try different guesser strategies, would we be able to beat our original lower bound?
If we find that our “optimal” strategy outperforms all of those search strategies proposed so far, it’s a fairly good suggestion that perhaps we have found a generally optimal strategy.
Let’s try it out:
from typing import Literal
import numpy.random as npr
def simulate_game_host(guest_strategy: Literal["optimal", "uniform", "midpoint", "midpoint_random"]) -> int:
lbnd = 1
ubnd = 100
reward = 6
# The host makes a single, optimal choice
ph = get_payoff(ubnd-lbnd+1).nash_eqs[0]
host_choice = np.random.choice(range(lbnd, ubnd+1), p=ph)
for _ in range(100):
reward -= 1
# our guest now makes choices similar to the host strategies from before
if guest_strategy == "optimal":
pg = get_payoff(ubnd-lbnd+1).nash_eqs[1]
guest_choice = np.random.choice(range(lbnd, ubnd+1), p=pg)
elif guest_strategy == "uniform":
guest_choice = np.random.choice(range(lbnd, ubnd+1))
elif guest_strategy == "midpoint":
guest_choice = int((lbnd+ubnd)/2)+1
assert guest_choice >= lbnd and guest_choice <= ubnd
elif guest_strategy == "midpoint_random":
# add a slight random variation into the search
guest_choice = int((lbnd+ubnd)/2)+1+np.random.choice(range(-2,3))
# bound our result
guest_choice = max(lbnd, min(ubnd, guest_choice))
if host_choice < guest_choice:
ubnd = guest_choice - 1
elif host_choice > guest_choice:
lbnd = guest_choice + 1
else:
return reward
if lbnd >= ubnd:
return reward - 1
return None
print("Optimal:")
print(np.mean([simulate_game_host("optimal") for _ in range(50000)]))
print("Uniform:")
print(np.mean([simulate_game_host("uniform") for _ in range(50000)]))
print("Midpoint:")
print(np.mean([simulate_game_host("midpoint") for _ in range(50000)]))
print("Midpoint random:")
print(np.mean([simulate_game_host("midpoint_random") for _ in range(50000)]))
The output we get here is:
Optimal:
-0.21954
Uniform:
-0.62518
Midpoint:
-0.2307
Midpoint random:
-0.24602
In other words, even when the host only chooses once, it appears that our optimal strategy outperforms all of the other search strategies that we tested originally. This suggests that our optimizations DO generalize to the original game… unfortunately, I don’t really have the proof to demonstrate it.
What’s the take-away?#
This probably isn’t a great question for interviews, it took me a few hours and some research just to get to an optimal answer… and it didn’t properly generalize. Fortunately, our host strategy is at least outperforming those that were suggested earlier – so we can say with (at least empirical) confidence that we’ve found a good, close-to-optimal answer at least.
Of course, to some extent this actually a great interview question because there are layers to the problem. A wide breath of experience enables engineers to look at problems in ways that the layman may never consider. There are a huge number of fields of math which can be transformative for solving even everyday problems at work, and many folks don’t realize just because they’ve never looked at a problem from that perspective.
If you do present this problem in an interview, I’d ask that you at least let the lower bound solution succeed. Let them start with \$6. Then all this math was worth it.